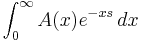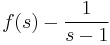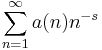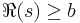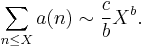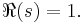Wiener–Ikehara theorem
The Wiener–Ikehara theorem can be used to prove the prime number theorem (PNT) (Chandrasekharan, 1969). It was proved by Norbert Wiener and his student Shikao Ikehara in 1932. It is an example of a Tauberian theorem.
Statement
Let A(x) be a non-negative, monotonic nondecreasing function of x, defined for 0 ≤ x < ∞. Suppose that
converges for ℜ(s) > 1 to the function ƒ(s) and that ƒ(s) is analytic for ℜ(s) ≥ 1, except for a simple pole at s = 1 with residue 1: that is,
is analytic in ℜ(s) ≥ 1. Then the limit as x goes to infinity of e−x A(x) is equal to 1.
Application
An important number-theoretic application of the theorem is to Dirichlet series of the form
where a(n) is non-negative. If the series converges to an analytic function in
with a simple pole of residue c at s = b, then
Applying this to the logarithmic derivative of the Riemann zeta function, where the coefficients in the Dirichlet series are values of the von Mangoldt function, it is possible to deduce the PNT from the fact that the zeta function has no zeroes on the line
References
- S. Ikehara (1931), "An extension of Landau's theorem in the analytic theory of numbers", Journal of Mathematics and Physics of the Massachusetts Institute of Technology 10: 1–12, Zbl 0001.12902
- Wiener, Norbert (1932), "Tauberian Theorems", Annals of Mathematics, Second Series 33 (1): 1–100, doi:10.2307/1968102, ISSN 0003-486X, JFM 58.0226.02, JSTOR 1968102
- K. Chandrasekharan (1969). Introduction to Analytic Number Theory. Grundlehren der mathematischen Wissenschaften. Springer-Verlag. ISBN 3-540-04141-9.
- Hugh L. Montgomery; Robert C. Vaughan (2007). Multiplicative number theory I. Classical theory. Cambridge tracts in advanced mathematics. 97. Cambridge: Cambridge Univ. Press. pp. 259–266. ISBN 0-521-84903-9.